There are only two correct ways to implement binary search. Here is the less known one.
int binary_search(int *nums, int len, int target) {
int l = -1;
int r = len;
while (l < r - 1) {
int mid = (l + r) >> 1;
if (nums[mid] < target) {
l = mid;
} else {
r = mid;
}
}
return r;
}
This version returns the index of the first element in nums that is greater than or equal to the target. If there is no such element, len will be returned.
Although only r is returned, l could also be of interest. It contains the index of the last element that is smaller than the target. if there is no such element, l will be -1, which is a good indicator for "no such element". It is always the case that r = l + 1 when the algorithm terminates.
Replace < with <=, l will be the last element that is smaller than or equal to the target, and r will be the first element that is greater than the target, subject to the same special cases above if there is no such element. If operator <= is not implemented, use !(target < nums[mid]) which is logically equivalent to nums[mid] <= target.
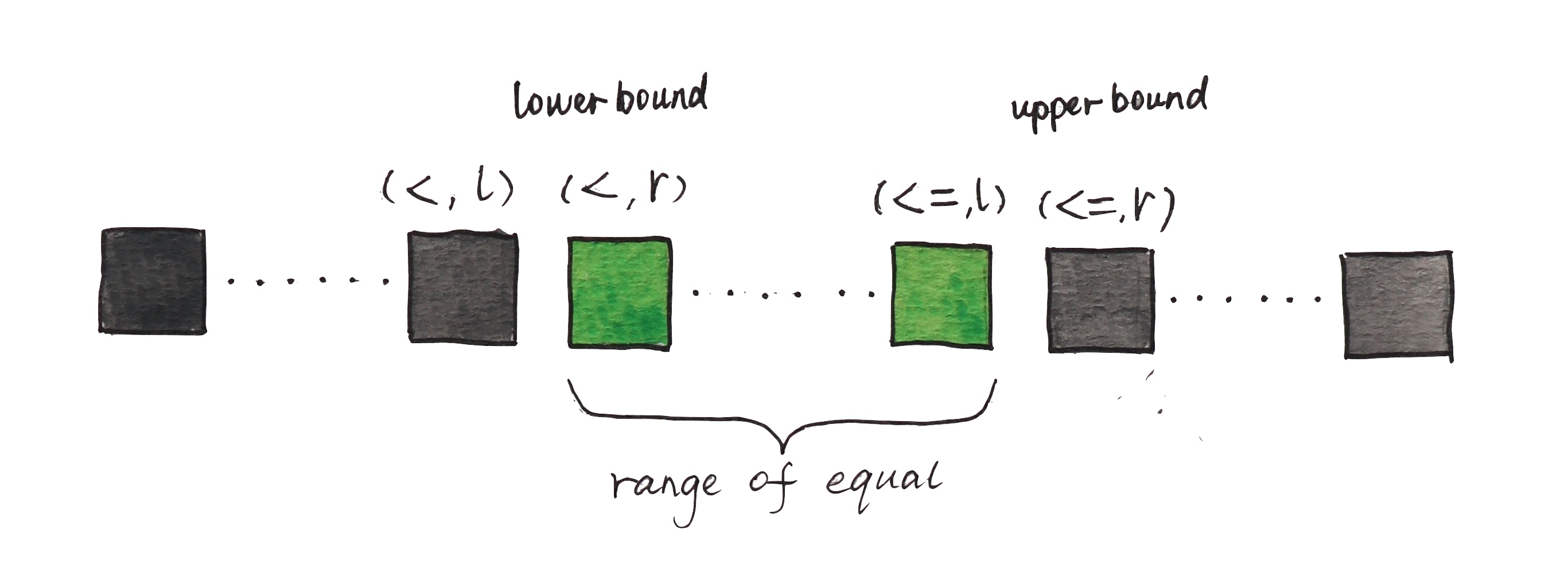
Note if there is only one element in nums that is equal to target, (<,r) and (<=,l) will converge. If target is not in nums, see the following picture.
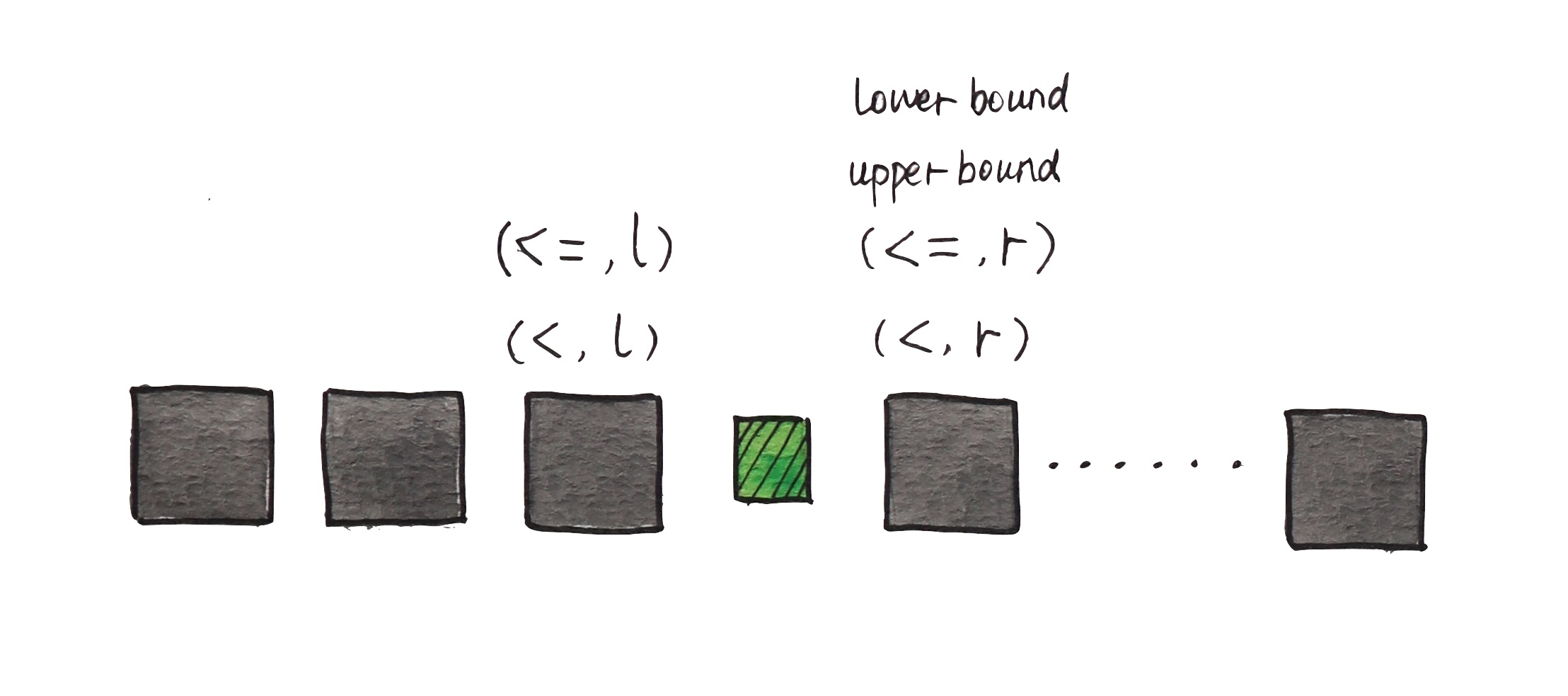
Or if you prefer precise definitions:
| op | symbol | is the | that is | or |
|---|---|---|---|---|
| < | l | last | smaller than (<) | -1 |
| <= | l | last | smaller than or equal to (<=) | -1 |
| < | r | first | greater than or equal to | len |
| <= | r | first | greater than | len |
The third line in the above table (<, r) implements lower_bound, while the fourth line (<=, r) implements upper_bound.
The drawback of this approach, is that the initially l is set to a special value -1. This might not always be possible if the index is of type usize. The advantage, is that neither l or r need to plus or minus one in each iteration, which leaves no room for error.
The other way
The other correct way of implementing binary search, is the approach used in lower_bound and upper_bound in C++ STL. It can be found on cppreference.com.
The interesting aspect of this implementation is that the two pointers started as a valid range [0, len), but terminated as an empty range [r, r), when l and r are equal. To me that makes the implementation harder to reason about. I acknowledge that you don't have to reason about it very often, though.
Criteria of being correct
To be correct, binary_search must return a reasonable value in all of the following cases, when looking for 2.
1 2 3
1 2
1 3
2 3
1
2
3
1 1 2 2 3 3
1 1 2 2
1 1 3 3
2 2 3 3
1 1
2 2
3 3You might also want to duplicate each case into a odd length one and an even length one.